ベルマンフォード(Bellman-Ford)法は単一始点最短経路問題のアルゴリズムの一種です。
ダイクストラ法との違いは、負の辺の取り扱いに対応しており、負の閉路の検出が可能である点です。
ただし、計算量はダイクストラ法の方が少ないため、負辺が存在しない場合は基本的にダイクストラ法を使用したほうが良いです。
Contents
アルゴリズム
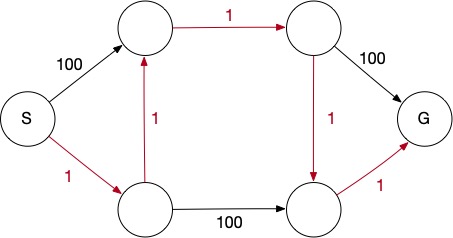
まず、閉路のない場合を考え、頂点数を|V|, 辺の数を|E|とします。
上のグラフの場合、|V| = 6、|E| = 8です。
始点から終点まで到達できる場合、最短経路の移動回数は高々|V-1|回です。
なぜなら今考えているグラフには負の閉路は存在しない為、1度訪れたノードに戻ることは無いからです。
(背理法で証明可能?)
さて、|V|-1回の更新で十分であることは分かりました。
あとは各頂点からについてどの頂点から来た場合が最小コストであるかを知る必要があります。。
そこで、「全ての辺について最小コストを更新をする」動作を|V-1|回繰り返せばどの頂点から来れば最小コストとなるのかが求まります。
↓「全ての辺について最小コストを更新をする」に該当するコード
for (int from = 0; from < n; from++) {
for (auto e : G[from]) {
// 更新
if (cost[e.to] > cost[from] + e.cost) {
cost[e.to] = cost[from] + e.cost;
}
}
}
実際その動作を行えば良く、オーダーはO(|V|*|E|)となります。
閉路の検出
嘘解法
「上記アルゴリズムを実行後、もう|V|回繰り返して終点のコストが更新されたら負の閉路が存在する」という解法を思い付きますが、実はこれでは不十分です。
反例
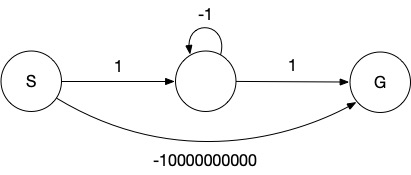
以下の例の場合を考えてみましょう。
(|V|-1)*|E|回の更新で、ゴールへ向かう最小コストは-10000000000であると求められます。
-1の負のループが存在し、実際の最小コストは-INFとなるわけですが、これ検出するには2*|V|*|E|回の更新では不十分であることがわかります。
(-10000000003回の更新を繰り返さないといけません)
正しい解法
「|V|-1回更新更新を行った後でも、始点から終点への経路上にある頂点の最小コストが更新可能である」場合に負の閉路が存在します。
「始点から終点への経路上にある頂点」とは、以下の性質を満たします。
- 始点からその頂点に到達可能
- その頂点から終点に到達可能
( = 逆辺のグラフで、終点からその頂点に向かうことが出来る)
1, 2はそれぞれDFSまたはqueueで求めることが可能です。
実装
const long long INF = 1LL << 60;
struct Edge {
int to;
ll cost;
};
using Graph = vector<vector<Edge>>;
vector<bool> can_reach(const Graph& G, int start) {
ll n = G.size();
vector<bool> ans(n);
queue<int> que;
que.push(start);
ans[start] = true;
while (!que.empty()) {
int index = que.front();
que.pop();
for (const auto& it : G[index]) {
if (ans[it.to] == false) {
que.push(it.to);
ans[it.to] = true;
}
}
}
return ans;
}
// Bellman Ford
// G: グラフ
// rev: 逆辺のグラフ(負の閉路検出用)
// start: 始点
// goal: 終点
// 戻り値: goalに行くまでの最小コスト。負の閉路が存在する場合は-INFとなる。
ll bellman_ford(const Graph& G, const Graph& rev, const int start, const int goal) {
const int n = G.size();
// 始点からそこまで行くのにかかるのコスト
vector<ll> cost(n, INF);
vector<ll> cost_middle;
cost[start] = 0;
// 閉路がなければn回のループで良いが、閉路検出用にn+1回回す
for (int i = 0; i < n; i++) {
// すべての辺を走査
for (int from = 0; from < n; from++) {
if (cost[from] == INF) {
continue;
}
for (auto e : G[from]) {
// 更新
if (cost[e.to] > cost[from] + e.cost) {
cost[e.to] = cost[from] + e.cost;
}
}
}
// 閉路検出用
if (i == n - 1) {
cost_middle = cost;
}
}
// 始点から到達できるか
auto can_reach_from_start = can_reach(G, start);
// 終点へ到達できるか
auto can_reach_from_goal = can_reach(rev, goal);
for (int i = 0; i < n; i++) {
if (can_reach_from_start[i] && can_reach_from_goal[i]) {
// 始点から終点へ移動できる経路上のノードの内、値が更新されるものが存在したら負のループが存在する。
if (cost_middle[i] != cost[i]) {
return -INF;
}
}
}
return cost[goal];
}
関連問題
- Coins Respawn (ABC137)